2.2 장에서, 강성 행렬과 컴플라이언스 행렬은 둘 다 36 개의 요소를 갖는 6×6 행렬임을 알 수 있었다. 그런데, 스트레인 에너지 밀도 함수 $ W $ 의 존재로 인하여 강성 행렬과 컴플라이언스 행렬은 대칭 행렬임을 보일 수 있다.
스트레인 에너지 밀도 함수 $ W $ 는 다음과 같이 정의된다.
$$ W = \frac{1}{2} C_{ij} \varepsilon_i \varepsilon_j $$
$ W $ 를 $ \varepsilon_i $ 와 $ \varepsilon_j $ 로 두번 미분하면, 미분 순서에 따라 아래와 같은 결과를 얻을 수 있다.
$$ \frac{\partial ^2 W}{\partial \varepsilon_i \partial \varepsilon_j}=C_{ij}, \qquad \qquad \frac{\partial ^2 W}{\partial \varepsilon_j \partial \varepsilon_i}=C_{ji} $$
그런데 미분 순서와 관계 없이 미분 값은 서로 같아야 하므로 $ C_{ij} = C_{ji} $ , 즉 강성 행렬은 대칭 행렬이 된다. 비슷한 방법으로 $ S_{ij} = S_{ji} $ 도 보일 수 있다.
따라서 강성 행렬은 아래와 같이 나타낼 수 있으며, 36개의 non-zero 값 중 독립적인 값은 21개가 된다.

여기에 재료가 가지고 있는 대칭성을 고려하면 추가적인 단순화가 가능하다.
1) monoclinic 재료
재료의 물성치가 어떤 하나의 평면에 대해 대칭인 재료를 monoclinic 재료라고 한다. 예를 들어 아래 그림과 같이 대칭면이 2-3 평면인 재료를 생각해 보자.
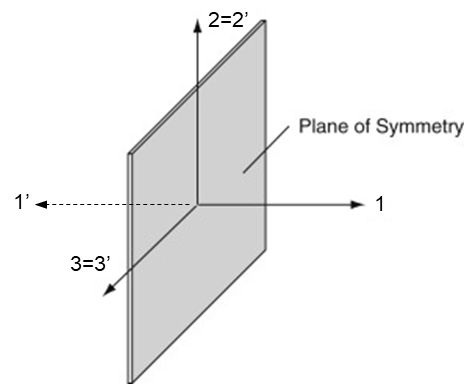
좌표 변환 행렬 $ [Q] $ 는 아래와 같이 계산된다.
$$ [Q] = \begin{bmatrix}
i_1’ \cdot i_1 & i_1’ \cdot i_2 & i_1’ \cdot i_3 \\
i_2’ \cdot i_1 & i_2’ \cdot i_2 & i_2’ \cdot i_3 \\
i_3’ \cdot i_1 & i_3’ \cdot i_2 & i_3’ \cdot i_3 \\
\end{bmatrix} = \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix} $$
그러면,
$$\begin{align*} [\sigma’] & = [Q][\sigma][Q]^T = \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix} \begin{bmatrix}
\sigma_{11} & \sigma_{12} & \sigma_{13} \\
\sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33} \\
\end{bmatrix} \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix} \\ & = \begin{bmatrix}
-\sigma_{11} & -\sigma_{12} & -\sigma_{13} \\
\sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33} \\
\end{bmatrix} \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix} = \begin{bmatrix}
\sigma_{11} & -\sigma_{12} & -\sigma_{13} \\
-\sigma_{21} & \sigma_{22} & \sigma_{23} \\
-\sigma_{31} & \sigma_{32} & \sigma_{33} \\
\end{bmatrix}
\end{align*} $$
즉,
$$ \begin{align*}
& \sigma_1’ = \sigma_1, \quad \sigma_2’ = \sigma_2, \quad \sigma_3’ = \sigma_3, \\
& \sigma_4’ (=\sigma_{23}’) = \sigma_4, \quad \sigma_5’ (=\sigma_{13}’) = -\sigma_5, \quad \sigma_6’ (=\sigma_{12}’) = -\sigma_6 \\
\end{align*} $$
비슷하게,
$$ \begin{align*}
& \varepsilon_1’ = \varepsilon_1, \quad \varepsilon_2’ = \varepsilon_2, \quad \varepsilon_3’ = \varepsilon_3, \\
& \varepsilon_4’ (=\gamma_{23}’) = \varepsilon_4, \quad \varepsilon_5’ (=\gamma_{13}’) = -\varepsilon_5, \quad \varepsilon_6’ (=\gamma_{12}’) = -\varepsilon_6
\end{align*} $$
이 재료의 강성 행렬 $ [C] $ 는 2-3 평면에 대해 대칭 변환을 시켜도 그 값이 변하지 않을 것이므로,
$$ [\sigma] = [C] [\varepsilon], \qquad [\sigma’] = [C] [\varepsilon’] $$
$$ \begin{matrix}
\begin{align*}
\sigma_1 & = C_{11} \varepsilon_1 + C_{12} \varepsilon_2 + C_{13} \varepsilon_3 + C_{14} \varepsilon_4 + C_{15} \varepsilon_5 + C_{16} \varepsilon_6 \\
\sigma_1’ = \sigma_1 & = C_{11} \varepsilon_1 + C_{12} \varepsilon_2 + C_{13} \varepsilon_3 + C_{14} \varepsilon_4 - C_{15} \varepsilon_5 - C_{16} \varepsilon_6 \end{align*} \\
\therefore C_{15}=C_{16}=0 \end{matrix} $$
$$ \begin{matrix}
\begin{align*}
\sigma_2 & = C_{21} \varepsilon_1 + C_{22} \varepsilon_2 + C_{23} \varepsilon_3 + C_{24} \varepsilon_4 + C_{25} \varepsilon_5 + C_{26} \varepsilon_6 \\
\sigma_2’ = \sigma_2 & = C_{21} \varepsilon_1 + C_{22} \varepsilon_2 + C_{23} \varepsilon_3 + C_{24} \varepsilon_4 - C_{25} \varepsilon_5 - C_{26} \varepsilon_6 \end{align*} \\
\therefore C_{25}=C_{26}=0 \end{matrix}$$
$$ \begin{matrix}
\begin{align*}
\sigma_3 & = C_{31} \varepsilon_1 + C_{32} \varepsilon_2 + C_{33} \varepsilon_3 + C_{34} \varepsilon_4 + C_{35} \varepsilon_5 + C_{36} \varepsilon_6 \\
\sigma_3’ = \sigma_3 & = C_{31} \varepsilon_1 + C_{32} \varepsilon_2 + C_{33} \varepsilon_3 + C_{34} \varepsilon_4 - C_{35} \varepsilon_5 - C_{36} \varepsilon_6 \end{align*} \\
\therefore C_{35}=C_{36}=0 \end{matrix} $$
$$ \begin{matrix}
\begin{align*}
\sigma_4 & = C_{41} \varepsilon_1 + C_{42} \varepsilon_2 + C_{43} \varepsilon_3 + C_{44} \varepsilon_4 + C_{45} \varepsilon_5 + C_{46} \varepsilon_6 \\
\sigma_4’ = \sigma_4 & = C_{41} \varepsilon_1 + C_{42} \varepsilon_2 + C_{43} \varepsilon_3 + C_{44} \varepsilon_4 - C_{45} \varepsilon_5 - C_{46} \varepsilon_6 \end{align*} \\
\therefore C_{45}=C_{46}=0 \end{matrix} $$
$$ \begin{matrix}
\begin{align*} \sigma_5 & = C_{51} \varepsilon_1 + C_{52} \varepsilon_2 + C_{53} \varepsilon_3 + C_{54} \varepsilon_4 + C_{55} \varepsilon_5 + C_{56} \varepsilon_6 \\
\sigma_5’ = -\sigma_5 & = C_{51} \varepsilon_1 + C_{52} \varepsilon_2 + C_{53} \varepsilon_3 + C_{54} \varepsilon_4 - C_{55} \varepsilon_5 - C_{56} \varepsilon_6 \end{align*} \\
\therefore C_{51}=C_{52}=C_{53}=C_{54}=0 \end{matrix} $$
$$ \begin{matrix}
\begin{align*} \sigma_6 & = C_{61} \varepsilon_1 + C_{62} \varepsilon_2 + C_{63} \varepsilon_3 + C_{64} \varepsilon_4 + C_{65} \varepsilon_5 + C_{66} \varepsilon_6 \\
\sigma_6’ = -\sigma_6 & = C_{61} \varepsilon_1 + C_{62} \varepsilon_2 + C_{63} \varepsilon_3 + C_{64} \varepsilon_4 - C_{65} \varepsilon_5 - C_{66} \varepsilon_6 \end{align*} \\
\therefore C_{61}=C_{62}=C_{63}=C_{64}=0 \end{matrix} $$
이상을 정리하면,
$$ \begin{equation} \begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \sigma_4 \\ \sigma_5 \\ \sigma_6 \end{bmatrix} =
\begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & 0 & 0 \\
& C_{22} & C_{23} & C_{24} & 0 & 0 \\
& & C_{33} & C_{34} & 0 & 0 \\
& & & C_{44} & 0 & 0 \\
& \text{SYM} & & & C_{55} & C_{56} \\
& & & & & C_{66} \end{bmatrix}
\begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \varepsilon_4 \\ \varepsilon_5 \\ \varepsilon_6 \end{bmatrix} \end{equation} $$
으로, non-zero 값을 갖는 행렬 요소는 20개이고, 그 중 독립 변수는 13개가 됨을 알 수 있다.
2) specially orthotropic 재료
대칭면이 모두 3개인 재료를 orthotropic 재료라고 하며, 특별히 좌표축과 재료의 대칭축이 서로 일치하는 경우를 specially orthotropic 이라고 한다.

monoclinic 재료 때 진행했던 방법과 유사하게, 이번에는 대칭면이 1-2 인 평면에 대하여 강성 행렬을 구해보면,
$$ \begin{matrix}
[Q] = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
\end{bmatrix} \\
[\sigma’] = [Q][\sigma][Q]^T = \begin{bmatrix}
\sigma_{11} & \sigma_{12} & -\sigma_{13} \\
\sigma_{21} & \sigma_{22} & -\sigma_{23} \\
-\sigma_{31} & -\sigma_{32} & \sigma_{33} \\
\end{bmatrix} \end{matrix}$$
$$ \begin{matrix}
\sigma_1’ = \sigma_1, \quad \sigma_2’ = \sigma_2, \quad \sigma_3’ = \sigma_3, \quad \sigma_4’ = -\sigma_4, \quad \sigma_5’ = -\sigma_5, \quad \sigma_6’ = \sigma_6 \\
\varepsilon_1’ = \varepsilon_1, \quad \varepsilon_2’ = \varepsilon_2, \quad \varepsilon_3’ = \varepsilon_3, \quad \varepsilon_4’ = -\varepsilon_4, \quad \varepsilon_5’ = -\varepsilon_5, \quad \varepsilon_6’ = \varepsilon_6
\end{matrix} $$
$$ \begin{matrix}
\begin{align*} \sigma_4 & = C_{41} \varepsilon_1 + C_{42} \varepsilon_2 + C_{43} \varepsilon_3 + C_{44} \varepsilon_4 + C_{45} \varepsilon_5 + C_{46} \varepsilon_6 \\
\sigma_4’ = -\sigma_4 & = C_{41} \varepsilon_1 + C_{42} \varepsilon_2 + C_{43} \varepsilon_3 - C_{44} \varepsilon_4 - C_{45} \varepsilon_5 + C_{46} \varepsilon_6 \end{align*} \\
\therefore C_{41}=C_{42}= C_{43}=C_{46}=0 \end{matrix} $$
$$ \begin{matrix}
\begin{align*} \sigma_5 & = C_{51} \varepsilon_1 + C_{52} \varepsilon_2 + C_{53} \varepsilon_3 + C_{54} \varepsilon_4 + C_{55} \varepsilon_5 + C_{56} \varepsilon_6 \\
\sigma_5’ = -\sigma_5 & = C_{51} \varepsilon_1 + C_{52} \varepsilon_2 + C_{53} \varepsilon_3 - C_{54} \varepsilon_4 - C_{55} \varepsilon_5 + C_{56} \varepsilon_6 \end{align*} \\
\therefore C_{51}=C_{52}=C_{53}=C_{56}=0
\end{matrix} $$
$$ \begin{equation} \therefore [C] = \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & C_{16} \\
& C_{22} & C_{23} & 0 & 0 & C_{26} \\
& & C_{33} & 0 & 0 & C_{36} \\
& & & C_{44} & C_{45} & 0 \\
& \text{SYM} & & & C_{55} & 0 \\
& & & & & C_{66} \end{bmatrix} \end{equation} $$
마지막으로 대칭면이 1-3 일 경우에는,
$$ \begin{equation} [C] = \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & C_{15} & 0 \\
& C_{22} & C_{23} & 0 & C_{25} & 0 \\
& & C_{33} & 0 & C_{35} & 0 \\
& & & C_{44} & 0 & C_{46} \\
& \text{SYM} & & & C_{55} & 0 \\
& & & & & C_{66} \end{bmatrix} \end{equation} $$
식 (1)~(3) 으로부터, specially orthotropic 재료의 강성 행렬 $ [C] $ 는,
$$ \begin{equation} [C] = \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\
& C_{22} & C_{23} & 0 & 0 & 0 \\
& & C_{33} & 0 & 0 & 0 \\
& & & C_{44} & 0 & 0 \\
& \text{SYM} & & & C_{55} & 0 \\
& & & & & C_{66} \end{bmatrix} \end{equation} $$
이고, 12개의 non-zero 값 및 9개의 독립 변수를 갖는 것을 확인할 수 있다.
※ generally orthotropic
그림 2.4 을 보면, x, y 축은 재료의 주축 1, 2 와 $ \theta $ 만큼 회전되어 있는 것을 볼 수 있다.
specially orthotropic 재료가 하나의 축을 기준으로 일정 각도만큼 회전되어 있는 것을 “generally” orthotropic 이라고 부르며, 독립 계수는 specially orthotropic 과 동일하게 9 개이나, monoclinic 재료처럼 20개의 non-zero 값을 갖는다.
3) specially orthotropic, transversely isotropic 재료
specially orthotropic, transversely isotropic 재료는 2-3 평면에서 재료 섬유가 임의 배치되어 있어, 1축 방향으로 회전을 하더라도 물성치가 동일하다.

앞에서 specially orthotropic 재료의 강성 행렬은 (4) 와 같이 계산하였다. 여기에서, transversely isotropic 재료의 경우 2축 3축 방향의 구분이 없기 때문에, 아래의 추가적인 구속 조건을 갖게 된다.
$$ C_{22}=C_{33}, \quad C_{12}=C_{13}, \quad C_{55}=C_{66} $$
그리고, 2-3 평면에서 수직 응력과 전단 응력이 서로 종속이므로, $ C_{44} $ 도 더이상 독립 변수가 아니다.
$ C_{44} $ 를 구하기 위하여 2-3 평면에서 순수 전단을 받고 있는 왼쪽과 같은 상태를 생각해 보자.

강성 행렬에서, 2-3 평면만 고려할 경우 관계식은 아래와 같다.
$$ \begin{bmatrix} \sigma_2' \\ \sigma_3' \\ \sigma_4' \end{bmatrix} = \begin{bmatrix} C_{22} & C_{23} & 0 \\ C_{23} & C_{22} & 0 \\ 0 & 0 & C_{44} \end{bmatrix} \begin{bmatrix} \varepsilon_2' \\ \varepsilon_3' \\ \varepsilon_4' \end{bmatrix} $$
따라서,
$$ \begin{equation} \sigma_2' = C_{22} \varepsilon_2' + C_{23} \varepsilon_3' \end{equation} $$
좌표 변환 행렬을 통해 x-y-z 좌표계에서 x'-y'-z' 좌표계로 변환하면, 아래와 같은 관계식이 성립한다.
$$ \begin{bmatrix} \sigma_2' \\ \sigma_3' \\ \sigma_4' \end{bmatrix} = \begin{bmatrix} c^2 & s^2 & 2cs \\ s^2 & c^2 & -2cs \\ -cs & cs & c^2-s^2 \end{bmatrix} \begin{bmatrix} \sigma_2 \\ \sigma_3 \\ \sigma_4 \end{bmatrix} $$
$$ \begin{bmatrix} \varepsilon_2' \\ \varepsilon_3' \\ \frac{\gamma_4'}{2} \end{bmatrix} = \begin{bmatrix} c^2 & s^2 & 2cs \\ s^2 & c^2 & -2cs \\ -cs & cs & c^2-s^2 \end{bmatrix} \begin{bmatrix} \varepsilon_2 \\ \varepsilon_3 \\ \frac{\gamma_4} {2} \end{bmatrix} $$
여기에서, $ c=\cos \theta, s=\sin \theta $ 이다. 위의 관계식에서,
$$ \sigma_2' = c^2 \sigma_2 + s^2 \sigma_3 + 2cs \sigma_4 = 2cs \sigma_4 $$
$$ \varepsilon_2' = c^2 \varepsilon_2 + s^2 \varepsilon_3 + 2cs (\frac{\gamma_4}{2}) = 2cs (\frac{\gamma_4}{2}) = cs \varepsilon_4 $$
$$ \varepsilon_3' = s^2 \varepsilon_2 + c^2 \varepsilon_3 - 2cs (\frac{\gamma_4}{2}) = -2cs (\frac{\gamma_4}{2}) = -cs \varepsilon_4 $$
이제 식 (5) 에 대입하여 정리하면,
$$ 2cs \sigma_4 = C_{22} cs \varepsilon_4 - C_{23} cs \varepsilon_4 $$
$$ \sigma_4 = \left ( \frac{C_{22}-C_{23}}{2} \right ) \varepsilon_4 $$
$$ \therefore C_{44} = \frac{C_{22}-C_{23}}{2} $$
이상을 정리하면, specially orthotropic, transversely isotropic 재료의 강성 행렬은
$$ \begin{equation} [C] = \begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\
& C_{22} & C_{23} & 0 & 0 & 0 \\
& & C_{22} & 0 & 0 & 0 \\
& & & \frac{C_{22}-C_{23}}{2} & 0 & 0 \\
& \text{SYM} & & & C_{66} & 0 \\
& & & & & C_{66} \end{bmatrix} \end{equation} $$
이고, 12개의 non-zero 값에 독립 변수는 5개를 갖는다.
4) isotropic 재료
isotropic 재료의 경우 모든 방향의 물성치가 동일하기 때문에,
$$ C_{11} = C_{22} = C_{33} \qquad C_{12} = C_{13} = C_{23} $$
$$ C_{44} = C_{55} = C_{66} = \frac{C_{11}-C_{12}}{2} $$
가 성립한다. 따라서 강성 행렬은,
$$ \begin{equation} [C] = \begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\
& C_{11} & C_{12} & 0 & 0 & 0 \\
& & C_{11} & 0 & 0 & 0 \\
& & & \frac{C_{11}-C_{12}}{2} & 0 & 0 \\
& \text{SYM} & & & \frac{C_{11}-C_{12}}{2} & 0 \\
& & & & & \frac{C_{11}-C_{12}}{2} \end{bmatrix} \end{equation} $$
이고, 12개의 non-zero 값에 독립 변수는 2개를 갖는다.
<종합>
여러 재료들에 대하여 여지까지 공부했던 것을 아래 표와 같이 정리할 수 있다.

'STUDY > 복합재료' 카테고리의 다른 글
| 3.1 Introduction (0) | 2022.10.12 |
|---|---|
| 2.6 Generally Orthotropic Lamina (0) | 2022.10.09 |
| 2.5 Specially Orthotropic Lamina (0) | 2022.10.08 |
| 2.4 Orthotropic and Isotropic Engineering Constants (1) | 2022.10.07 |
| 2.2 Effective Moduli in Stress-Strain Relationships (0) | 2022.10.05 |