재료의 한 점에서의 일반적인 3차원 응력 분포는 아래 그림과 같다.

여기에서 응력은 $ \sigma_{ij} $ 의 꼴로 표현되는데, 첫번째 인덱스 $ i $ 는 응력이 작용하는 면, 두번째 인덱스 $ j $ 는 응력의 작용 방향을 나타낸다.
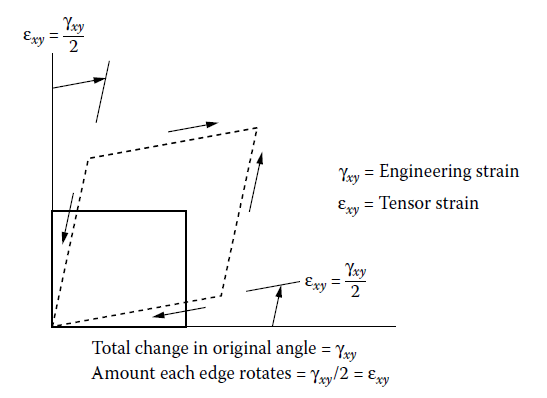
변형률도 응력과 동일하게 정의한다. 한 가지 주의할 점은 텐서 변형률 $ \varepsilon_{ij} $ 와 엔지니어링 변형률 $ \gamma_{ij} $ 을 구별해야 한다는 것이다. 두 변형률은 수직 방향에 대해서는 서로 동일하나, 전단 변형률에서는 아래와 같은 차이가 있다.
일반적으로 응력은 변형률에 강성을 곱하여 계산 가능하다. 만약 아주아주 일반적인 상황을 가정하여, 한 점에서의 9 가지 응력이 한 점에서의 9 가지 변형률과 모두 관계가 있다고 한다면, 응력과 변형률은 아래와 같은 관계를 가진다고 할 수 있다.

즉, 강성 행렬 $ \left [ C \right ] $ 는 81개의 요소를 갖는 9×9 행렬이다.
그런데, 응력과 변형률 모두 $ \sigma_{ij}=\sigma_{ji} $, $ \varepsilon_{ij}=\varepsilon_{ji} $ 가 성립한다. 따라서 응력과 변형률은 각각 9 가지가 아니라 6 가지라고 볼 수 있으며, 표기의 단순화를 위하여 아래와 같이 표기를 재 정의하기로 한다.

이제 강성 행렬 $ \left [ C \right ] $ 는 6×6 행렬이 되며, 36개의 요소를 갖는다.
이것을 행렬식으로 표현하면 아래와 같다.
$$ \left \{ \sigma \right \}=[C] \left \{ \varepsilon \right \} $$
또는, 아래와 같이 표현할 수도 있다.
$$ \left \{ \varepsilon \right \}=[S] \left \{ \sigma \right \} $$
여기에서 $ [S] $ 는 강성 행렬의 역행렬로, 컴플라이언스 행렬이라고 부른다.
재료의 강성 행렬과 컴플라이언스 행렬은 위치에 따라 다르지만, 재료의 거시적인 움직임을 분석하기 위해서 아래와 같이 평균 응력/변형률을 고려하는 것이 편리하다.

평균 응력 $ \bar{\sigma} $ 와 평균 변형률 $ \bar{\varepsilon} $ 의 관계로부터 얻어지는 강성 행렬과 컴플라이언스 행렬을 "유효 계수 (effective moduli)" 라고 한다.
'STUDY > 복합재료' 카테고리의 다른 글
| 3.1 Introduction (0) | 2022.10.12 |
|---|---|
| 2.6 Generally Orthotropic Lamina (0) | 2022.10.09 |
| 2.5 Specially Orthotropic Lamina (0) | 2022.10.08 |
| 2.4 Orthotropic and Isotropic Engineering Constants (1) | 2022.10.07 |
| 2.3 Symmetry in Stress-Strain Relationships (0) | 2022.10.06 |