09. 2차 선형 상미분 방정식 - 자유 진동 (mass-spring-damper system)

2차 ODE 의 대표적인 문제로 매스-스프링-댐퍼 시스템을 들 수 있다.

1. undamped system

먼저 그림 1 과 같이 단순한 mass-spring 시스템에 대해 생각해 보자.

좌표계는 질량이 정적 평형 상태에 있을 때 (즉, 스프링의 복원력과 질량의 중량이 같을 때) 를 기준으로 하고, 아래쪽 방향을 + 로 생각한다.

$y$ 를 질량의 변위라고 하면, 질량이 $y$ 의 위치에 있을 때 이 것은 위쪽 방향으로 스프링의 복원력 만큼의 힘을 받게 된다.

즉, $F = -k y$ 이다. 뉴턴의 제 2 법칙인 $F = m a$ 를 이 질량에 적용하면 아래와 같다.

$$a = d^2 y / d t^2 = y'' \qquad -ky = m y''$$

$$\begin{equation} my'' + ky = 0 \end{equation}$$

 

이 방정식의 특성 방정식과 그 해는,

$$\lambda ^2 + \frac{k}{m} = 0$$

$$\lambda = \pm i \omega_0, \qquad \omega_0=\sqrt {\frac {k}{m}}$$

 

따라서 이 방정식의 일반 해는 아래와 같다.

$$\begin{equation} y(t) = A \cos \omega_0 t + B \sin \omega_0 t \end{equation}$$

 

일반 해는 cos 법칙을 사용하면 아래와 같이 표현할 수도 있다.

$$y(t)=C \cos (\omega_0 t - \delta), \qquad C=\sqrt{A^2+B^2}, \quad \tan \delta = B/A$$

 

그림 3

그림 3 은 몇 가지 초기 값에 대해 해를 도시한 그래프이다. 주파수 $f = \omega_0/2\pi$ 로 조화 진동하는 것을 볼 수 있다.

이 주파수 $f$ 를 시스템의 고유 주파수라고 부른다.

 

2. damped system

앞서 살펴본 undamped system 에서 질량은 영원히 진동을 멈추지 않는다. 현실에서는 이런 일은 벌어지지 않는데, 그것은 바로 댐퍼의 존재 (공기 마찰, 스프링 손실 등) 때문이다.

역학에서, 댐퍼에 의한 힘은 속도에 비례하는 것으로 생각한다. 즉, $F_\text{damp}= -cy'$ 이다.

이 힘을 식 (1) 에 추가하면 우리는 mass-spring-damper 시스템의 식을 아래와 같이 얻을 수 있다.

$$\begin{equation} my'' + cy' + ky = 0 \end{equation}$$

 

이 ODE 의 특성 방정식과 그 해는 아래와 같다.

$$\lambda ^2 + \frac{c}{m} \lambda + \frac{k}{m} = 0$$

$$\lambda = -\frac{c}{2m} \pm \frac{1}{2m}\sqrt{c^2-4mk}$$

 

나중을 위해 $\alpha= \frac{c}{2m}$,  $\beta = \frac{1}{2m}\sqrt{c^2-4mk}$ 로 두자.

 

이제 이 방정식의 일반 해는 루트 안의 값 $(c^2-4mk)$ 에 따라 아래의 세 가지 경우로 나뉜다.

1) $c^2-4mk >0$ : 서로 다른 두 실근 (overdamping)

2) $c^2-4mk =0$ : 중근 실근 (critical damping)

3) $c^2-4mk <0$ : 두 허근 (underdamping)

 

1) 과도 감쇠 (overdamping)

서로 다른 두 실근을 가질 때 일반해는 아래와 같다.

$$\begin{equation} y(t) = c_1 e^{-(\alpha-\beta)t}+ c_2 e^{-(\alpha+\beta)t} \end{equation}$$

 

아래의 그림 4는 몇 가지 초기 값에 대해 그래프를 그려본 것이다.

과도한 댐핑 (overdamping) 으로 인하여 시스템은 진동하지 않고, 빠른 속도로 평형 위치 $(y=0)$ 으로 접근한다.

그림 4

 

2) 임계 감쇠 (critical damping)

중근을 가질 경우 일반해는 아래와 같다.

$$\begin{equation} y(t)=(c_1+c_2t)e^{-\alpha t} \end{equation}$$

 

이 경우 댐핑은 임계 값을 가지는데, $c$ 의 값이 여기에서 조금만 작아져도 $c^2-4mk$ 의 값이 음수가 되며, 시스템은 진동하기 시작한다.

그래프로 표현하면 아래의 그림 5와 같으며, 과도 감쇠 경우와 거의 비슷하다는 것을 알 수 있다.

그림 5

 

3) 부족 감쇠 (underdamping)

$c^2-4mk <0$ 일 경우 $\beta$ 의 값은 허수가 된다.

$$\beta = i \omega^* \qquad \text{where} \qquad \omega^*=\frac{1}{2m}\sqrt{4mk-c^2}=\sqrt{\frac{k}{m}-{c^2}{4m^2}}$$

 

특성 방정식의 두 근은 $\lambda = -\alpha \pm i \omega^*$ 이며, 일반해는 아래와 같다.

$$\begin{equation} y(t)=e^{-\alpha t} (A \cos \omega^* t + B \sin \omega^* t) = Ce^{-\alpha t} \cos (\omega^* - \delta) \end{equation}$$

 

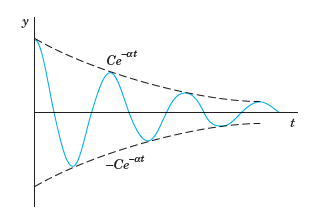
이 것을 그래프에 도시하면 아래 그림 6과 같다.

변위 $y$ 는 점선으로 표시된 상하 점근선 $y=\pm C e^{-\alpha t}$ 내에서 진동하며 감쇠되는 것을 볼 수 있다.

그림 6