미분 방정식은 문제에 따라 해가 없을 수도 있고, 하나만 있을 수도, 심지어 무한히 많을 수도 있다.
미분 방정식의 문제 풀이 전에 해의 존재 유무와 유일한지 여부를 미리 알 수 있다면 큰 힘이 될 것이다.
$$ \begin{equation} y'=f(x,y), \qquad y(x_0)=y_0 \end{equation} $$
위와 같은 초기값 문제를 풀 때, 해의 존재성, 유일성과 관련하여 아래의 두 정리가 있다.
정리1. 해의 존재성 정리
사각형 영역 $R: \left | x-x_0 \right \vert <a, \quad \left | y-y_0 \right \vert <b$ 를 생각하자.
1) $f(x,y)$ 가 $R$ 에서 연속이고,
2) 유계(bounded)일 때, 즉, $\left | f(x,y) \right \vert \le K, \quad \forall (x,y) \in R$ 인 $K$ 가 존재할 때,
초기값 문제 (1) 은 $\left | x-x_0 \right \vert < \alpha$ 에서 최소한 하나 이상의 해를 갖는다.
※ $ \alpha = \min \left ( a, b/K \right )$
참고로 정리1 에서 $R$ 의 영역을 도시하면 아래와 같다.
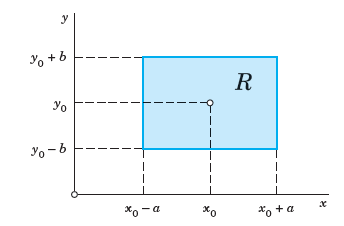
이 정리를 간략히 표현하면 아래와 같다.

$ f(x,y) $ 가 유계라는 의미는 곧 $y$ 의 기울기가 최소 $-K$ 에서 최대 $K$ 로 제한되어 있다는 얘기이다.
문제에서 주어진 초기값 $(x_0, y_0)$ 로부터 기울기가 $-K$ 와 $K$ 인 직선 $l_1$, $l_2$ 를 그리면 위의 그림과 같다.
해의 그래프는 그림의 파란색 음영 내에 존재해야 하며, 영역의 크기와 기울기에 따라 해의 존재성이 보장되어 있는 구간 $\alpha$ 가 달라진다.
정리2. 해의 유일성 정리
사각형 영역 $R$ 에서
1) $f(x,y)$ 와 $f_y = \partial f / \partial y$ 가 연속이고,
2) 유계(bounded)일 때, 즉,
(a) $\left | f(x,y) \right \vert \le K$, (b) $\left | f_y(x,y) \right \vert \le M \quad \forall (x,y) \in R$
인 $K$ 와 $M$ 이 존재할 때,
초기값 문제 (1) 은 $\left | x-x_0 \right \vert < \alpha$ 의 구간에서 유일한 해를 갖는다.
'STUDY > 공학수학' 카테고리의 다른 글
| 08. 2차 선형 상미분 방정식 - 계수가 상수인 경우 (0) | 2022.09.16 |
|---|---|
| 07. 2차 선형 상미분 방정식 - Homogeneous ODE (0) | 2022.09.15 |
| 05. 1차 상미분 방정식 - orthogonal trajectory (0) | 2022.09.14 |
| 04. 1차 상미분 방정식 - 선형 상미분 방정식 (1) | 2022.09.14 |
| 03. 1차 상미분 방정식 - 완전 상미분 방정식, 적분 인자 (0) | 2022.09.10 |