05. 1차 상미분 방정식 - orthogonal trajectory

orthogonal trajectory 는 번역하면 직교 절선이라고 한다는데, 너무 생소하니 그냥 원어 표기를 유지하도록 하겠다.

예를 들어 아래와 같은 타원의 방정식이 있다고 하자.

$$\frac{1}{2}x^2+y^2=c$$

 

$c>0$ 인 $c$ 에 대하여 타원 군을 아래 그림과 같이 작도할 수 있다.

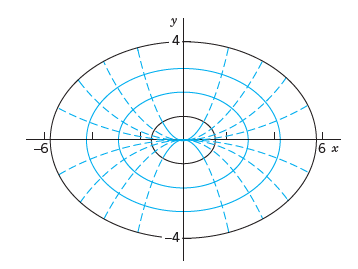
상미분 방정식을 이용하면 모든 타원에 수직인 orthogonal trajectory 들을 구할 수 있다. (그림의 점선 부분)

먼저 타원위의 점 $(x,y)$ 에서 타원의 기울기는 아래와 같이 구할 수 있다.

$$x+2yy'=0$$

$$y'=-\frac{x}{2y}$$

 

orthogonal trajectory 의 기울기는 타원의 기울기와 곱하여 -1 이 되어야 하므로,

$$ \tilde{y}'=\frac{2\tilde{y}}{x}$$

 

이제 변수 분리법을 이용하여 위의 미분 방정식을 풀 수 있다.

$$ \frac {d \tilde{y}}{ \tilde{y}}=2 \frac{dx}{x}, \qquad \ln \left | \tilde{y} \right \vert = 2 \ln x +c, \qquad \tilde{y}=c^*x^2$$